در نظر بسیاری از مردم، حل مسئله عالیترین نمونهٔ اندیشیدن است. در کار حل مسئله میکوشیم به هدفی برسیم ولی وسیلهٔ حاضر و آمادهای برای این کار در اختیار نداریم. باید هدف را به پاره هدفها و این پاره هدفها را نیز به هدفهای جزئیتر تقسیم کنیم تا سرانجام بهسطحی برسیم که ابزار دستیابی برای ما مهیا است (آندرسون، ۱۹۹۰).

نکات فوق را میتوان با مثال سادەای توضیح داد. فرض کنید مجبور هستید شمارهٔ رمز قفلی را کشف کنید. تنها اطلاعی که در اختیار دارید این است که شمارهٔ رمز عددی چهار رقمی است و با رسیدن بههر رقم صحیح صدای تلق خواهید شنید. هدف کلی، کشف شمارهٔ رمز است. بسیاری از مردم بهجای آنکه سعی کنند همزمان هر چهار رقم را با روش کورمال کشف کنند، نخست هدف کلی را بهچهار پاره - هدف تقسیم میکنند که هریک مربوط به یکی از ارقام شمارهٔ رمز است. نخستین پاره هدف، پیدا کردن رقم اول است. برای اینکار، شما روش خاصی در پیش میگیرید: قفلگردان را به آرامی میچرخانید و در عین حال منتظر شنیدن صدای تلق هستید. پاره هدف دوم، پیدا کردن رقم دوم است و برای اینکار همان شیوهٔ قبلی را بهکار میگیرید. در مورد سایر پاره هدفها نیز بههمین شیوه عمل میکنید.
راهبردهائی که مردم برای تجزیهٔ هدفها به پارههدفها برمیگزینند از موضوعات اساسی در حل مسئله است. نکتهٔ مهم دیگر نحوهٔ بازنمائی (representation) مسئله است چون این نیز عامل مؤثری در حل مسئله محسوب میشود.
راهبردها در حل مسئله
بخش عمدهٔ اطلاعات ما درباهٔ راهبردهای مربوط به تجزیه هدفها حاصل پژوهشهای نیوول (Newell) و سیمون (Simon) (۱۹۷۲) است. برای این منظور، معمولاً پژوهشگر از آزمودنی میخواهد در حین حل مسئلهای دشوار، افکار خود را با صدای بلند برزبان آورد. پژوهشگر آنگاه پاسخهای کلامی آزمودنی را تحلیل میکند تا سرنخهائی دربارهٔ راهبردهای او بهدست آورد. از این راه، چند راهبرد عمومی شناسائی شده است.
یکی از راهبردها این است که تفاوت وضعیت موجود در موقعیت مشکلزا را با وضعیت هدف که همان صورت حلشدهٔ مسئله است، کاهش دهیم. حالا بار دیگر مسئلهٔ قفل رمزدار را در نظر آورید. در آغاز کار وضعیت موجود هیچ اطلاعی از هیچیک از ارقام رمز نداریم، در حالیکه در وضعیت هدف هر چهار رقم رمز را شناسائی کردهایم. بههمین دلیل نیز کاهش تفاوت این دوحالت را بهعنوان پاره هدف انتخاب میکنیم. این پاره هدف با پیدا کردن نخستین رقم رمز تحقق مییابد. حال آگاهی از نخستین رقم رمز نیز بخشی از وضعیت موجود داست، اما هنوز تفاوتی بین وضعیت موجود و وضعیت هدف وجود دارد که برای کاهش آن به پیدا کدن دومین رقم رمز میپردازیم، و بههمین شیوه، کار را ادامه میدهیم. بنابراین، فکر زیربنائی در روش کاهش تفاوت این است که خرده هدفی تعیین کنیم که با دستیابی به آن در موقعیتی نزدیکتر بههدف قرار میگیریم.
راهبردی مشابه ولی پیچیدهتر نیز هست که تحلیل وسیله - هدف (means - ends analysis) نام دارد. در این راهبرد، وضعیت موجود با وضعیت هدف مقایسه میشود تا مهمترین تفاوت این دو وضعیت مشخص گردد. اینک خرده هدف اصلی ما از میان برداشتن این تفاوت است. حالا باید وسیله یا روشی برای دستیابی به این خرده هدف پیدا کرد. ممکن است بهچنین روشی دست یابیم ولی متوجه شویم که استفاده از آن در وضعیت موجود میسر نیست. به این ترتیب حل این مشکل تازه، خرده هدف جدیدی میشود. در بسیاری از موقعیتهای حل مسئله از چنین راهبردی استفاده میشود. بهنمونهٔ زیر توجه کنید:
باید پسرم را به مهدکودک برسانم. تفاوت عمده بین وضعیت فعلی و وضعیت دلخواه من، در چیست؟ فاصله. چه چیزی میتواند این فاصله را از میان بردارد؟ اتومبیل. اتومبیلم روشن نمیشود. برای روشن کردن آن چه چیزی لازم است؟ باطری نو. برای پیدا کردن باطری نو چه چیزی لازم است؟ کارگاه تعمیر اتومبیل (اقتباس از نیوول و سیمون، ۱۹۷۲، نقل از آندرسون، ۱۹۹۰، ص ۲۳۲).
تحلیل وسیله - هدف شیوهای پیچیدهتر از روش کاهش تفاوت است، چون امکان میدهد حتی دست به اقدامی بزنیم که ممکن است بهطور موقت همانندی وضعیت موجود را با وضعیت هدف کاهش دهد. در مثال بالا احتمال دارد کارگاه تعمیر اتومبیل در سمتی مخالف مسیر مهدکودک قرار گرفته باشد و بههمین جهت رفتن به آنجا موقتاً ما را از هدف دورتر سازد، اما در هرحال گامی ضروری برای حل مسئله محسوب میشود.
راهبرد دیگر این است که کار را از هدف شروع کنیم و رو به عقب برویم. این روش مخصوصاً در حل مسائل ریاضی کارآمد است که نمونهای از آن را در شکل نمونهای از مسئلههای هندسه میبینید. صورت مسئله از این قرار است: اگر شکل ABCD مستطیل باشد، ثابت کنید دو ضلع AD و BC برابر هستند. با روش رو بهعقب بهشرح زیر عمل میکنیم:
چه اطلاعاتی لازم است تا ثابت شود که دو خط AD و BC برابر هستند؟ برای اثبات برابری این دو خط باید ثابت کنیم که دو مثلث ACD و BDC با هم مساوی هستند (congruent). یکی از راههای اثبات تساوی این دو مثلث این است که ثابت کنیم دو ضلع و یک زاویه آنها برابر است (اقتباس از آندرسون، ۱۹۹۰، ص ۲۳۸).
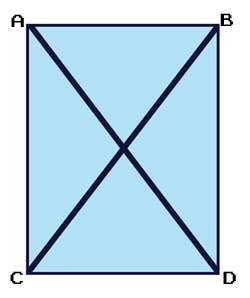
برای حل این مسئله استدلال ما از هدف در جهت خرده هدف (اثبات تساوی دو مثلث) و از این خرده هدف در جهت خرده هدف دیگر (اثبات برابری دو ضلع و یک زاویهٔ دو مثلث) جریان مییابد و این فرآیند آنقدر تکرار میشود تا سرانجام به خرده هدفی برسیم که وسیلهٔ حاضر و آمادهای برای رسیدن به آن در دست است.
سه راهبرد مورد بحث، یعنی کاهش تفاوت، تحلیل وسیله - هدف، و استدلال رو بهعقب، بسیار قابل تعمیم هستند و میتوان از آنها در حل تقریباً هر مسئلهای استفاده کرد. این راهبردها که گاه روشهای ضعیف خوانده میشوند، مبتنی بر هیچ دانش ویژهای نیستند و حتی احتمال دارد فطری باشند. ما از این روشهای ضعیف مخصوصاً در مراحل اولیهٔ یادگیری مبحثی جدید یا بههنگام برخورد به مسائلی با محتوای ناآشنا استفاده میکنیم. اندکی بعد خواهیم دید که پس از کسب تخصص در هر رشته، آدمها از روشهای قوی (و نیز بازنمائیهای قوی) خاص رشتههای تخصصی استفاده میکنند - روشهائی که بهتدریج جانشین روشهای ضعیف میشوند (آندرسون، ۱۹۸۷).

