آمار توصيفى را عمدتاً مفاهيمى از قبيل جدول توزيع فراوانى و نسبتهاى توزيع، نمايش هندسى و تصويرى توزيع، اندازههاى گرايش به مرکز، اندازههاى پراکندگى و نظاير آن تشکيل مىدهد. آمار توصيفى براى تبيين وضعيت پديده يا مسئله يا موضوع مورد مطالعه مورد استفاده قرار مىگيرد يا در واقع ويژگىهاى موضوع مورد مطالعه به زبان آمار تصويرسازى و توصيف مىگردد. در اينجا محقق پس از استخراج اطلاعات اقدام به خلاصه کردن و طبقهبندى دادههاى آمارى مىنمايد و اين کار را با تشکيل جداول توزيع فراوانى انجام مىدهد و اگر بخواهد تجزيهوتحليل را به کمک رايانه انجام دهد، به آن برنامه مىدهد. پس از تشکيل جداول توزيع فراوانى محقق مىتواند درصدهاى توزيع فراوانى و درصدهاى تراکمى را محاسبه کند. براى نمايش نحوهٔ توزيع صفت در نمونه يا جامعه روشهاى گوناگونى وجود دارد. محقق بسته به نياز و علاقهاى که دارد، مىتواند دادهها را به تصوير بکشد. اين کار باعث درک سريعتر خواننده يا بيننده از واقعيت و نحوهٔ توزيع صفت مىگردد.
روشهاى متداول براى نمايش تصويرى نحوهٔ توزيع صفت در جامعه عبارتند از:
۱. روش هيستوگرام يا نمودارهاى ستونى ساده و ترکيبى (افقى و عمودى).
۲. روش پلىگون يا نمودارهاى چند ضلعى ساده و ترکيبى.
۳. روش منحنى براى دادههاى تراکمى و تجمعى (فراوانى تراکمى و درصدهاى تراکمى).
۴. روش قطاعى يا شعاعى و دايرهاى ساده و ترکيبي.
۵. روش نمودار مثلثى.
۶. روش منحنى نمايش سرىهاى زمانى.
۷. روش نمايش فضايى و پراکندگى پديده در فضا در شکل نقشههاى جغرافيايى تراکمى.
۸. نمايش ترکيبى ستونى و نشانهاى پراکندگى پديده در فضا روى نقشهٔ جغرافيا.
۹. نمايشهاى تخيلى و تصويرسازى متناسب با بزرگى و کوچکى پديده در فضا.
۱۰. نمايش سلسله مراتبى و روابط يک سويه يا دو سويه پديدهها.
۱۱. نمودارهاى هرمى براى نمايش ساختمان جمعيت.
۱۲. نمودارهاى تصويرى براى نمايش شکلى پديدهها.
محقق مىتواند کار تصويرسازى توزيع صفت را يا با دست يا با رايانهها انجام دهد. طبعاً، استفاده از رايانه در تجزيهوتحليل دادهها باعث ساعتها صرفهجويى در وقت محققان براى ترسيم اشکال و نمودارهاى جالب مىشود. بعد از مرحله تصويرسازي، محقق مىتواند اندازههاى گرايش به مرکز را براى دادههاى آمارى محاسبه نمايد. او مىتواند اين کار را با دست يا با رايانه انجام دهد. اندازههاى گرايش به مرکز که عمدتاً شامل ميانگين، ميانه و نما هستند، معرف نحوهٔ همگرايى توزيع صفتند.
ميانگين از تقسيم حاصل جمع نمرهها بر تعداد آنها بدست مىآيد. ميانگين يا معدل معمولاً به شکل (x̄) براى نمونه و به شکل () براى جامعه آمارى نمايش داده مىشود. معدل نمرههاى طبقهبندى نشده از فرمول x=x۱+x۲+x۳...xn / n بدست مىآيد. علامت x نمرهٔ هر فرد يا طبقه است.
معدل نمرههاى طبقهبندى شده از فرمول x=Σxi Fi / n بدست مىآيد. در اين فرمول Fi ، فراوانى هر طبقه، Xi ، نمرهٔ هر طبقه يا نقطه ميانى هر طبقه و Σ ، مجموع (سيگما) است. نما، اندازهٔ گرايش به مرکز، در توزيع نمرهاى است که بيشتر از بقيه نمرهها تکرار شده باشد و به آن مُد نيز گفته مىشود. براى محاسبه از فرمول زير استفاده مىشود:
| d۱ | |||||
| ) | ( | L + C | Mo = | ||
| d۱ + d۲ |
که در آن L ، کرانهٔ پايين طبقهاى که نما در آن قرار دارد؛ Mo ، مد يا نما؛ d۲ ، تفاضل فراوانى مطلق طبقهٔ نمادار از طبقه مابعد؛ d۱ تفاضل فراوانى مطلق طبقه نمادار از طبقهٔ ماقبل (در صورتى که جدول توزيع بطور صعودى مرتب شده باشد.) و C فاصله طبقات است.
ميانه، يکى ديگر از اندازههاى گرايش به مرکز، پارامترى است که فراوانى مقادير يا توزيع نمرهها را به دو گروه تقسيم مىکند و خود، نمرهٔ ميانى را تشکيل مىدهد؛ يعنى اگر دادهها و نمرهها بطور صعودى يا نزولى مرتب شده باشند، نمره وسط ميانه است که از فرمول زير محاسبه مىگردد:
| N | ||||||||
| ) | - F C | ( | ||||||
| ۲ | ||||||||
| ) C | ( | L + | Md = | |||||
| Fi | ||||||||
در اين فرمول N ، تعداد دادهها؛ Md ، فراوانى مطلق طبقهاى که ميانه در آن قرار دارد؛ L، کرانه پايين طبقهاى که ميانه در آن قرار دارد؛ C ، فاصله طبقات و FC ، فراوانى تجمعى ماقبل (در صورتى که جدول توزيع فراوانى بطور صعودى مرتب نشده باشد.) طبقهاى که ميانه در آن قرار دارد است.
همچنين، محقق مىتواند اندازههاى پراکندگى را محاسبه نمايد. اين اندازهها عبارتند از: دامنهٔ تغيير، انحراف استاندارد و واريانس. دامنهٔ تغيير سادهترين اندازه پراکندگى است که مبيّن تفاوت بين بزرگترين و کوچکترين نمرهٔ توزيع است. انحراف استاندارد يا انحراف معيار يک اندازهٔ پراکندگى است که به موقعيت نسبى هر نمره در توزيع فراوانى بستگى دارد. در واقع انحراف استاندارد به محاسبهٔ انحراف از ميانگين هر يک از نمرهها بستگى دارد و از فرمول زير محاسبه مىگردد:
| ∑ ( X - µ)۲ | √ | ||
| σ = | |||
| N |
| ∑( x - x̄)۲ | √ | ||
| S = | |||
| n |
(x-x̄)، انحراف از ميانگين هر نمره؛ S، انحراف استاندارد يا انحراف معيار؛ x، ميانگين؛ x̄، نمره و n حجم نمونه است.
انحراف استاندارد و واريانس از پارامترهاى مهم پراکندگى هستند و در تجزيهوتحليل دادهها چه در روش توصيفى و چه در روش استنباطى کاربرد زيادى دارند. واريانس جامعه يا نمونه آمارى در حقيقت مجذور انحراف معيار آن است و از فرمول زير محاسبه مىشود:
| ∑( x - x̄)۲ | ||
| S۲ = | ||
| n |
| ∑ ( X - µ)۲ | ||
| σ ۲= | ||
| N |
واريانس شاخصى است که نشان دهندهٔ تفاوتها و پراکندگى نمرهها است و تغييرپذيرى نمرهها را نشان مىدهد؛ يعنى اينکه نمرهها تا چه اندازه ناهمگون هستند و تا چه حد با يکديگر تفاوت دارند. هرچه واريانس کمتر باشد، تجانس و هماهنگى و همگونى بيشتر است، و برعکس.
انحراف استاندارد نيز شاخص پراکندگى يا تغييرپذيرى نمرهها است و مىتوان گفت که هرقدر بزرگتر باشد تغييرپذيرى آنها بيشتر و برعکس هرقدر کمتر باشد تغييرپذيرى يا پراکندگى کمتر است، هرچند بزرگى و کوچکى انحراف استاندارد امرى نسبى است.
يکى از محاسن عمدهٔ انحراف استاندارد، رابطهاى است که بين واحد انحراف استاندارد و طرز قرار گرفتن نمرهها در منحنى طبيعى (نرمال) موجود است. به علت وجود چنين رابطهاى مىتوان از انحراف استاندارد بعنوان ملاکى براى مقايسهٔ گروههاى مختلف يا موقعيت فردى خاص استفاده کرد. (روشهاى مقدماتى آمارى در روانشناسى و تعليم و تربيت؛ ص ۹۲)
منحنى طبيعى يک منحنى قرينهاى است که شکلى شبيه زنگ يا زنگوله دارد؛ يعنى اکثر نمرهها در وسط انباشته شده است، بهطورى که در انتهاى دو طرف، دنبالهٔ نسبتاً طويلى بوجود مىآورد. مىتوان گفت منحنى طبيعى يک منحنى فراوانى است که نمرههاى متصل روى محور افقى و فراوانىها روى محور عمودى آن قرار مىگيرد. در صورتىکه نمرهها برحسب انحراف استاندارد تقسيمبندى شوند، مىتوان درصد افرادى را که بين دو نمره يا بين ميانگين و نمرهاي، يا بالاتر و پايينتر از نمرهاى جاى مىگيرند محاسبه کرد. (روشهاى مقدماتى آمارى در روانشناسى و تعليم و تربيت؛ ص ۹۳)
همچنين از منحنى طبيعى در موقعيتهايى که استنباطها با توجه به پارامترهاى جامعهٔ آمارى انجام مىگيرد (در حالى که تنها آمارهاى نمونه در دست است) مىتوان استفاده نمود. منحنى طبيعى داراى خصوصيات زير است:
۱. داراى يک نما است و ميانگين، ميانه و نما در آن ارزش يکسان دارند.
۲. نسبت به مرکز خود قرينه است.
۳. بر دو پارامتر ميانگين و انحراف استاندارد اتکا دارد.
۴. سطح کل زير منحنى مىتواند در فاصله بين دو مقدار از x بصورت درصد کل نمونه يا جامعه آمارى بيان شود.
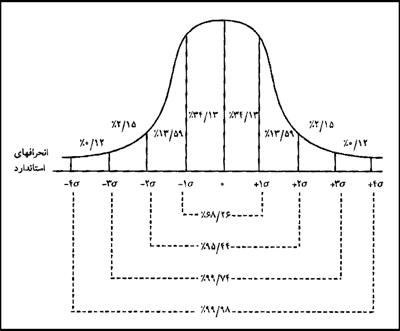
۵. حدود ۷/۹۹ درصد جامعه آمارى بين ۳ انحراف استاندارد قرار مىگيرد. (توسعه مهارتهاى تحقيقاتى در آموزش فنى و حرفهاي؛ مادول ۸، ص ۱۹/۱/۸.)
۶. حدود ۶۸/۲۶ درصد جامعه آمارى بين ۱ انحراف استاندارد و ۵/۹۵ درصد آنها بين ۲ انحراف استاندارد قرار دارند.
فاصلهاى که با انحراف استاندارد اندازهگيرى شده است و بين ميانگين و محور افقى قرار دارد، با علامت Z نشان داده مىشود (انحراف طبيعى يا نمرات استاندارد). در هر منحنى طبيعى با ميانگين و انحراف استاندارد معين، فاصله x از ميانگين مىتواند با استفاده از فرمول σ/x- =Z به نمره استاندارد يا سيگمايى يا تراز شده تبديل شود. در اين فرمول Z، نمره استاندارد؛ x نمرهٔ خام؛ ميانگين جامعه و σ ، انحراف استاندارد است.
Z مىتواند بسته به مقدار x مثبت يا منفى باشد. (روشهاى مقدماتى آمارى در روانشناسى و تعليم و تربيت؛ ص ۲۳/۱/۸)